Андрей Чернов
ЗОЛОТО
ПАРФЕНОНА (1,2,3)
глава из книги
В Афины со своей совой.
Древнегреческая
поговорка
В
ПОИСКАХ МЕРЫ

Фото с сайта http://www.adam-carr.net/travelindex16.html
Афинский Акрополь стоит на вершине
плоской, но высокой скалы (156 м над уровнем моря; 300 м в длину и 170 м в
ширину). Это место древнейшего поселения в Аттике. В крито-микенский период (XV–XIII вв. до н. э.) здесь была царская
резиденция.
Микенская культура пала, когда с севера
пришли племена ахейцев, а затем дорийцев. Но варвары на удивление быстро
цивилизовались. За несколько столетий в Греции появляется и вызревает тот тип
культуры, который никак нельзя отнести к разряду архаических.
Греки, как дети, но дети
любознательные. Они легкомысленны и болтливы, они тянут в дом, что ни попадя,
и, черпая сокровища знаний из древней мудрости Востока (в первую очередь
Египта) присваивают все, что нравится. Но каждое новое заимствование приводит
к еще большей новизне и самобытности античной культуры. И эту культуру
отличает то, что она никак не связана с загробным культом. Перед нами
покоящаяся на архаическом фундаменте рабовладения, но ведомая жаждой познания
и жаждой прекрасного светская культура свободных граждан.
В VII в. до н. э. Акрополь превращается в
гигантскую стройку. При тиране Писистрате (560–527 гг.) на месте царского дворца
возводится храм богини Афины. Когда в 480 г. Акрополь разрушен персами,
афиняне клянутся его восстановить. Персы отброшены, и в 447 г. Перикл,
поручив осуществление проекта скульптору Фидию, начинает строительство храма
Девы Афины.
ВЫПИСКИ ИЗ ЭНЦИКЛОПЕДИЙ И СЛОВАРЕЙ:
Парфенон – (греч.
Parthenón, от parthénos – дева), храм богини Афины Парфенос в
Афинах.
Построен на Акрополе в 447-438 до н. э.
Иктином и Калликратом; скульптурная отделка велась под руководством Фидия,
окончена в 432 до н. э. П. представляет собой мраморный дорический периптер
(30,89 м на 69,54 м[1]);
в его наосе, окруженном с трёх сторон двухъярусной колоннадой, находилась
хрисоэлефантинная статуя Афины работы Фидия. С запада к наосу примыкала
сокровищница, где хранилась казна Афинского морского союза. Фриз фасада был
украшен метопами с изображениями кентавромахии, амазономахии и гигантомахии,
фронтоны – скульптурными композициями (тема восточного фронтона – миф о
рождении Афины, западного – спор Афины и Посейдона из-за господства над
Аттикой). П.
отличался исключительной соразмерностью частей, синтезом дорического и
ионического ордеров, ясной величественностью и глубокой человечностью
архитектурных и скульптурных образов. П. подвергся разрушению в 1687 при
осаде Акрополя венецианцами во время войны с турками. В 1801–03 большая часть
скульптуры П. была вывезена в Великобританию и в 1816 помещена в Британский
музей в Лондоне (БСЭ).
Периптер (греч. peripteros – окруженный
колоннами; от peri – вокруг и pterón – крыло, боковая колоннада), тип
древнегреческого храма. Это прямоугольное в плане здание, с четырёх сторон
обрамленное колоннами.
Наос (греч. naós) – главное помещение древнегреческого
храма, святилище, где стояли статуи богов. Римляне называли наос целлой (лат.
cella). В православии наосом называется основное помещение церкви от главного
(западного) входа до алтаря. В наосе
Парфенона, окруженном с трёх сторон двухъярусной колоннадой,
находилась хрисоэлефантинная (золото плюс слоновая кость) статуя Афины работы
Фидия
Опистодом (греч. opisthódomos –
находящиися в задней части дома) – закрытое помещение в западной части
древне-греческого храма.
ПАРАДОКС
ВИТРУВИЯ
Задача состоит не в том, чтобы видеть то, чего никто не видел; а в том, чтобы об очевидном думать так, как никто не думал.
Эрвин Шрёдингер, нобелевский лауреат 1933 г.
за создание волновой механики атомного ядра
В архитектуре
параллельно существуют два противоположных взгляда на меру и пропорцию. Один
можно назвать модульным (или целочисленным), другой геометрическим (или
иррациональным). Первый подход проще и, конечно, древнее. Он предполагает,
что пропорции «совершенного» строения определяет некая, многократно
повторенная в нем идеальная единица меры.
Сторонники
геометрического подхода возражают: модуль, может быть, и существует, но
только как эталон самой меры, а пропорция рождается из геометрического
построения и потому не сводится к целочисленным отношениям (в идеале, а не на
строительной площадке, где об иррациональном думать некогда, а геометрический
замысел должен быть или выражен через целочисленные отношения, то есть
переведен некую в линейную меру).
Спор
сторонников модуля и сторонников пропорции возникший, видимо, сразу же, после
открытия несоизмеримости стороны квадрата и диагонали, напоминает куда менее
древнюю полемику о природе света, разделившую ученый мир на
«корпускулярников» и «волновиков». Но у физиков вопрос был закрыт, когда в
1905 году Эйнштейн показал, что свет, хотя и распространяется как непрерывная
волна, в некоторых случаях может вести себя и как поток частиц. То есть фотон
– и частица (корпускула), и волна одновременно.
О
модуле, как правило, любят рассуждать инженеры, конструкторы, прорабы и
архитекторы, работающие в типовом строительстве, а о геометрии
архитекторы-реставраторы и собственно архитекторы. (Разделение на
архитекторов и инженеров существовало уже в античности: считается, скажем,
что Иктин был архитектором Парфенона, а стройкой руководил его коллега
Калликрат.)
Мастера,
возводившие античные шедевры, были скупы на слова, поскольку их творения
говорили сами за себя. Но во второй половине I века до н. э. некто
Витрувий Поллион поднес Юлию Цезарю трактат «Десять книг об архитектуре». Он
писал: «Мы же, придерживаясь должного порядка,
излагаем все так, как тому научились от наших наставников, чтобы тот, кто,
следуя этим принципам, пожелает приступить к работе, имел в своем
распоряжении установленные пропорции, пользуясь которыми он мог бы правильно
и безупречно строить храмы по дорийскому образцу...»[2].
Чему же научили малоизвестного (так он сам себя
аттестует) архитектора его современники-наставники и те древние авторы,
которых мы, увы, знаем только по именам? Читаем дальше: «Фасад дорийского храма с той стороны, где размещаются колонны,
надлежит разделять, если это четырехколонник, на двадцать семь частей[3], а если шестиколонниик,
– на сорок две части. Одна из этих частей будет модулем, по-гречески
εμβατης; когда этот модуль установлен, то на
основании его производят вычисления всех частей постройки»[4].
По самой своей психологии Витрувий – инженер и
модулепоклонник (типичный «корпускулярник»). Его модуль и есть базовая
единица меры, укладывающаяся в фасаде n число раз.
По Витрувию толщина колонн
должна равняться двум модулям, высота вместе с капителью четырнадцати, высота
капители – один модуль, ширина – два и одна шестая[5].
Из этого следует, что отношение ствола колонны к ширине капители даст
пропорцию 6 к 1. Это натуральное (целочисленное) отношение, и Витрувий не
замечает, что в нем скрыта пропорция двойного мажорного золота, которую дает
отношение половины колонны к ширине капители:
14
: 2 : 2,166667 = 3,231 → 3,236 =
(√5 + 1)
Витрувий
утверждает: «Если природа сложила человеческое
тело так, что его члены по своим пропорциям соответствуют внешнему его
очертанию, то древние были, очевидно, вполне правы, установив, что при
постройках зданий отдельные их члены должны находиться в точной соразмерности
с общим видом всей фигуры. Поэтому, передав нам во всех своих произведениях
надлежащие правила их построения, они сделали это в особенности для храмов
Богов, так как и достоинства и недостатки этих зданий обычно остаются навеки»[6].
Все
верно, только под соразмерностью здесь понимаются целочисленные отношения. И
потому по рецепту Витрувия Парфенон можно лишь построить (но не
спроектировать!). То, что нам предлагает римский писатель, – азы
профессионального знания прораба, а не архитектора. Подмена искусства
архитектуры инженерной схемой (Витрувий называет в качестве автора этой схемы
некоего Гермогена) и сведéние гармонии к целочисленной схеме и выдает
сугубо утилитарный подход автора, задача которого перевести в камень то, что
сочинил зодчий.
Если б
возводивший Парфенон прораб Калликрат работал в одиночку и решился бы
«подправить» архитектуру зодчего Иктина, наверное, первое, что бы он сделал,
это расставил колонны Парфенона «правильно», то есть на равном расстоянии
друг от друга. Но «правильное» ядро фасада Парфенона составляют шесть
центральных колонн, а две крайние не только чуть толще (на множитель живого
ростового квадрата 1,03 к 1), но и расстояние от них до соседних меньше шага
рядовой колонны.
Высота
колонн к двум шагам трех крайних – пропорция 4 к 3, то есть пропорция катетов
священного треугольника 3–4–5. Исправь это, и Парфенон перестанет дышать,
перестанет искривлять окружающее его пространство и превратится в аккуратную
горку мраморных кубиков.
Витрувий
не хочет говорить об иррациональном. Другое дело – о том, что поверхность
стилобата должна быть чуть выпуклой (это называется курватурой), об энтасисе
– утолщении тела колонна на определенной высоте. Об иррациональном Витрувий,
скорее всего, знает, но в популярном труде, написанном для Цезаря, не считает
уместным повествовать о проблеме несоизмеримости стороны и диагонали
квадрата, или о задаче среднепропорционального деления отрезка. Во всяком
случае, в десяти своих книгах он упоминает о Парфеноне («храме Минервы») и
архитекторе Иктине только вскользь.
Почему
же в латинском мире, начиная с Возрождения, Витрувий входит в обязательную
программу архитектурного обучения?
Невостребованный
и, видимо, посредственный архитектор оказался блистательным писателем. Его
книга легка и талантлива. Из нее читатель узнавал, какие на небе есть
созвездия, а на земле ветры, как в бане Архимед открыл свой знаменитый закон
(«на тело, погруженное в жидкость и т. д.») и многое другое, не имеющее
прямого отношения к архитектуре. В частности, Витрувий невольно развеивает
миф о том, что античность не знала прямой перспективы, открытой якобы лишь
теоретиками Возрождения: «...скенография есть
рисунок фасада и уходящих вглубь сторон путем сведения всех линий к центру,
намеченному циркулем»[7].
Отметим
еще, что Витрувий мыслит исторически и излагает все, что ему известно, не для
того, чтобы понравиться Цезарю, а для того, чтобы передать знания потомкам.
Но – подчеркнем еще раз – он менее всего архитектор и теоретик архитектуры.
Он строитель и инженер-теоретик. И лучше всего это можно показать на примере
его отношения к числу π. Витрувий знает и пишет о нем. Но вот в каком
контексте: «Мы переходим теперь, в порядке
замысла нашего сочинения, к прибору не бесполезному, а чрезвычайно искусному,
унаследованному от предков, при помощи которого мы, сидя в повозке или плывя
по морю, можем узнавать, сколько миль мы проехали. Делается это так. Пусть
колеса повозки имеют четыре фута в поперечнике, так что если у колеса имеется
отметка, от которой оно начинает вращаться вперед по поверхности дороги, то,
повернувшись до той же отметки, с которой началось вращение, оно покроет
расстояние в двенадцать с половиной футов»[8].
Далее описывается устройство, состоящее из трех вращающихся барабанов, из
которого при четырехстах оборотах колеса в прикрепленный под днищем повозки
медный сосуд выпадает по одному круглому камешку.
При
таком приближении π рано не 3,14, а 3,125 (и потому обод обычного колеса
получается на два сантиметра короче реального). Но Витрувия это не заботит.
Ошибка в полпроцента представляется ему несущественной. И она действительно
приемлема, если речь о расстоянии, которое должна преодолеть когорта
легионеров или повозка купца. И грозит обрушением, если речь о возведении
купола или арки.
Самое
трудное в сюжете любой эволюции – это поиск переходного звена.
Но, как это не редко бывает с уникальными (и
потому непонятыми) экспонатами, звено может быть давным-давно найдено, только
лежит оно не в витрине, а в музейных запасниках.
Так, полагаю, случилось и с мерой Парфенона.
Если верить
Плутарху, афинский Парфенон называли Гекатомпедон – Стофутовый. (Сегодня
принято считать, что Плутах ошибся, но мы этого мнения не разделяем.)
Как
определить модуль, равный футу?
В 1762
г. сотрудники Британского общества любителей древностей Джеймс Стюарт и Николас Ревет начали
публикацию монументального труда «Афинские древности». Они и решили воспользоваться
методом своего соотечественника Исаака Ньютона, который установил размеры
египетского царского локтя по кратности габаритам погребальной камеры Хеопса.
Стюарт
и Ревет взяли размер фасада Парфенона по ширине стилобата (верхняя ступенька
основания, на которую опираются колонны храма) и, разделив на сто, получили
фут в 0,309 м[9].
Однако еще
в 1765 году на Акрополе археологами была найдена смета строительства другого
акропольского храма – Эрехтейона (это последний храм Акрополя, построенный в 421–405 гг. до н. э.). В 1927 году, сопоставив
размеры Эрехтейона и текст сметы, Г. Стевенс вывел размер фута в 0,325 м[10].
Позднее размер уточнили, а сам фут назвали дорийским (или дорическим).
Критики
гипотезы Стюарта и Ревета ссылаются на то, что «стофутовым» мог называться не
нынешний афинский Парфенон, а его предшественник, недостроенный и разрушенный
Ксерксом. Однако фундаменты этого храма не соответствуют ста дорийским
футам, и потому Вильям Белл Динсмур предположил, что Гекатомпедон – название
от еще более раннего храма, то есть «деда Парфенона»[11].
Впрочем, на Афинском Акрополе следов этого загадочного «дедушки» не
обнаружено.
А.
В. Радзюкевич вслед за шотландским историком Джимом
Коултоном[12]
приравнивает высоту антаблемента Парфенона (это карниз + фриз +
архитрав) к 10 дорийским футам (по 0,326867 м; далее – дф) и полагает, что локоть к футу относится
как 3 : 2, а высота колонны с капителью равна 31,5 футам либо 21 локтю.

При
дорийском локте (далее – дл) в 0,4903 м высоту антаблемента можно представить
и более точно:
3
дл ∙ 65/29 = 3,297 м
где
65/29 – целочисленное приближение к √5
Да и
некоторые другие величины Парфенона кратны дорийскому локтю (к примеру,
высота ордера 13,728 м, то есть 28 дорийский локтей).
Но
высота колонны с капителью 10,43, а не 10,3 м (это был бы 21 дл).
А. В.
Радзюкевич пишет: «Проведем сопоставление полученных
проверочных модулей с известными античными метрологическими стандартами,
такими как дорийский фут (около 0,327 м); ионический фут (около 0,297 м);
дорийский локоть (около 0,49 м); ионический локоть (около 0,44 м) и царский локоть (около 0,525 м). В результате
проверки полученных шести модулей на кратность этим величинам, получаем, что
только один вариант можно признать истинным по данному метрологическому
критерию. По данной интерпретации
габариты архитравной балки выражаются через 1/8 дорийского фута
(0,04085 м)»[13].
Однако толщина архитравной балки, на
которой лежит фриз храма, равна не 1,307 м (4 раза по 0,327 м), а 1,35 м.
Отклонение очевидно и существенно.
Итак, дорийский локоть и на других
замерах Парфенона дает прекрасный результат, а вот фут в 2/3 от него –
нулевой.
Значит, надо искать другое решение.
Если
строители Парфенона работали парной мерой (дорийским локтем и неким футом),
то искомая мера и есть открытый Стюартом и Реветом олимпийский фут (далее – оф).
Начнем с
уникальных обмерных чертежей Парфенона, опубликованных перед Второй мировой
войной греческим инженером-строителем Николаосом Баланосом (эта работа заняла
у него более тридцати лет)[14]. Ширина стилобата Парфенона (верха платформы, на которой
он стоит) – 30,875 м. Тогда длина олимпийского фута
– 0,30875 м.
Попытаемся
уточнить эту величину. Высота ордера Парфенона (высота колонн с капителями
плюс антаблемент), равная по обмерам 13,728 м, – это 28 дорийских локтей, а
тело колонны (колонна без капители) – 31 олимпийский фут (далее – оф).
Поскольку
высоту ствола колонны строители должны были вымерять куда более тщательно,
чем ширину стилобата, получим следующее значение фута:
9,570 м : 31 = 0,30871 м
Значит,
ширина стилобата как раз и дает 100 олимпийских футов.
И.
Ш. Шевелев, которому в 2000 году я сообщил об этой интерпретации, обратил мое
внимание на то, что мера в 31 фут совсем не случайна, ведь отношение
горизонтали стилобата и вертикали ствола колонны дает двойное мажорное
золото:
100 : 31 = 3,23 → (√5 +1)
= 3,24
Но
на это можно возразить, что зрительно ствол колонны продолжен ее шейкой (до
верха шейки идут каннелюры), и тогда отношение горизонтали стилобата к
единственной акцентированной вертикали храма ближе к π, чем к двойному
мажорному золоту.
Сведем
обмеры в таблицу.

ВЕРТИКАЛИ
ПАРФЕНОНА
100 оф,
деленные на 2,25, дают высоту ордера в 28 дл. Откл. от 100 оф : 2,25 лишь 7 мм.
Высота
ордера, деленная на √2, дает высоту каннелюры..
Высота
храма, деленная на Ф, дает величину
стереобат + колонна с капителью. Откл.
9 мм.
Сумма
высоты колонны с капителью + стереобат, деленная на Ф, дает высоту антаблемент + фронтон.
Откл. 13 мм.
Высота
фронтона (с толщиной кровли), деленная на Ф2/2,
дает высоту антаблемента. Откл. 5 мм
Высота
цоколя (фундамент + стереобат), деленная на Ф2/2, дает высоту стереобата. Откл. 4 мм
Ширина
ската крыши, деленная на Ф, дает
высоту колонны..
Пропорция
высоты каннелюр к толщине карниза – 10Ф
к 1.
Ширина
евтентерия (33,8 м), деленная на Ф,
дает две высоты колонны.
Высота
стереобата, деленная на π, дает высоту карниза. Откл. ок. 4 мм.
Ширину
стилобата Парфенона мы получаем и в дорийских локтях, и в олимпийских футах.
Но это может быть только при условии, что локоть и фут составляют парную меру
(странную для нас, со школьной скамьи привыкших к разделению: эталон метра
сам по себе, пропорция, измеряемая в абсолютных величинах, – сама по себе).
И
действительно, олимпийский фут, – это парная (диагональная) мера к дорийскому
локтю, заимствованная греками у древних египтян. (Восходит она
непосредственно к локтю Хесира.) 9 олимпийских футов – диагональ квадрата со
стороной в 4 дорийских (дорических) локтя. См. систему Модульных квадратов в
главе «Имхотеп = Хесира (3)»:
А БЫЛ ЛИ ФУТ?
Историк архитектуры А. В. Радзюкевич,
некогда вслед за К. Н. Афанасьевым сам пытавшийся интерпретировать размеры
первых русских храмов с помощью олимпийского фута[15],
через два десятилетия в электронной полемике на сайте http://www.a3d.ru/disput/61 поставил под сомнение и само существование
этой меры, и то, что она восходит как минимум к эпохе Парфенона и Эрехтейона.
Примеры употребления фута в 3,09 см в
постройках эллинистической эпохи приводит М. И. Максимова[16]. Отмечая, что в различных греческих
государствах фут имел неодинаковую длину и «большинство основных измерений
храма Афины Паллады в Приене (IV
в. до н. э.) делится почти без остатка на величину аттического фута, равную
0,295 м» (с. 60), автор приводит
десятки размеров, которые могут быть получены лишь при помощи олимпийского
фута.
«Размеры
кирпичей у греков, по словам Витрувия, были следующие: квадратные кирпичи,
равные 4 пядям, т. е. одному греческому футу (0.309 м), и квадратные кирпичи
в 5 пядей, т. е. 1 1/4 фута (0,386 м). Кроме того, применялись и половинчатые
кирпичи» (с. 45).
Здесь
стоит сделать оговорку, ведь в переводе Ф. А. Петровского текст Витрувия звучит так:
«Кирпич бывает трех сортов: один,
называемый по-гречески лидийским, – это применяемый у нас, длиною в полтора
фута, шириною в фут. Из остальных двух сортов строятся здания у греков. Один
из них называется πενταδωρον,
другой τετραδωρον.
Δωρον же греки называют пядь, потому что
δωρον по-гречески значит даяние, а его всегда несут
в пяди руки. Таким образом, кирпич пяти пядей в квадрате называется
пентадорон, а четырехпядевый – тетрадорон, и общественные здания строятся из
пентадорона, а частные – из тетрадорона» (Витрувий. Кн. II. Гл. 3; 3)[17].
Речь тут,
конечно, не о «пяди» (не о четверти аршина, и не о расстоянии между
оттопыренными большим и указательным пальцем), а о длани (ширине ладони, «пальме»).
Если древнеегипетская пальма равнялась 0,075 м (это 1/7 царского и 1/6
простого локтя), то греческая пальма (длань) в четверть олимпийского фута
должна быть 0,077 м.
Однако
далее Максимова пишет:
«Кирпичи, обнаруженные при раскопках
городских стен в Элевсине, несколько отличаются от этих размеров. Они равны
0,45 × 0,45 × 0,10 м. Одна строительная надпись из Элевсина
(вторая половина IV в.) предписывает употреблять кирпичи длиною в 0,492 м.
Размеры кирпичей, из которых сложена была найденная в Херсонесе печь
эллинистической эпохи, были: 0,55 м длины, 0,10 м толщины и от 0,13 до 0,19 м
ширины. Из этих примеров видно, что, вопреки свидетельству Витрувия,
стандартных размеров на кирпичи у греков не было и что размеры и форма
кирпичей не были постоянны».
Увы,
приведенные размеры говорят о том, что для Витрувия 0,45 м – это, скорее
всего, и есть «четырехпядевый тетрадорон» (4 раза по 0,1125 м), а 0,55 м –
пентадорон из пяти «пядей» (5 раз по 0,11 м). И тогда олимпийский фут тут ни
при чем.
Парижский инженер Огюст
Шуази в главе «Пропорции, перспектива и живописность в греческом искусстве»
своей «История архитектуры»[18] указывает, что «в Афинах крепостная
стена отличалась более простой, но, может быть, и более совершенной
структурой: кирпичная стена, покоившаяся на каменном основании в 11 футов
толщины» (имеются в виду греческие
«олимпийские» футы).
Вот и М. И. Максимова пишет следующее: «…ограничимся описанием конструкции односкатной крыши, на
примере крыши галереи на городских стенах Афин, восстановление которой дано
американским археологом Каскей (Caskey)[19] на основании строительной
надписи 306 г. до н. э. Общая ширина галереи на Афинских стенах равнялась
шести греческим футам, т. е. 1,85 м. <…> На расстоянии 0,62 м в стене
были проделаны окна, ширина которых также равнялась 0,62 м. Перемычки под
окнами состояли из двух рядов деревянных планок, которые поддерживались
вертикальными брусками, образующими косяки окон. На внутренней стороне
галереи помещались на расстоянии 1,85 м один от другого столбы из саманных
кирпичей шириной в 0,31 м. Таким образом, столбы приходились против каждого
второго простенка внешней стены галереи. Столбы эти имели высоту 2,47 м
<…> Внешние края стропил и лежащие на лих брусья были прикрыты снаружи
терракотовыми плитами, прибитыми к стропилам железными гвоздями. Общий наклон
крыши равнялся примерно 0,309 м на 1,85 м ширины крыши» (с. 96–97). Здесь каждый из восьми вышеприведенных размеров –
свидетельство использования олимпийского фута.
Однако это всего лишь реконструкция, и
потому вопрос об олимпийском футе по-прежнему следует считать открытым.
Куда
убедительней другие примеры М. И.
Максимовой:
Пилястры,
составляющие основание арки ворот городского рынка Приены середины II в. до
н. э. имеют высоту в 3,09 м, то есть десять олимпийских футов, а высота
клинообразных камней известняка и их толщина в нижней части, из которых
слагается арка – 0, 61 м, т. е. 2 оф (с. 82).
Ширина
плинты (нижняя часть цоколя, подошва стены) в арсенале Пирея 0,92 м (3 оф), а
высота ее 0.46 м, т. е. 1,5 оф (с. 90).
А теперь
перелистаем последнюю работу патриарха современной архитектурной метрологии
Кирилла Николаевича Афанасьева (1909–1992) и сделаем несколько выписок[20].
Цитирую по http://www.rusarch.ru/afanasiev2.htm
Стилобат Парфенона, измеренный по
верхней кромке, имеет меньшие стороны (восточного и западного фасадов),
равные по обмеру 30,89 м, что равно ста греческим олимпийским футам (1
греческий фут = 308.28 мм; 308,28 мм х 100 = 30 м 83 см)(11). Несомненно, что
именно этот размер следует признать исходным для последующего построения всех
соразмерностей формы храма. Об этом свидетельствует, прежде всего
"круглое" число футов (100)
…
Малый дорический ордер Пропилей имеет
высоту, равную 7,70 м (или 25 греч. футам).
…
Эрехтейон. Если южную стену храма по длине
разделить на равные четыре части, то мы получим продольный размер портика
Кариатид. (по обмеру также 5,58 м). Но это 18 оф = 5,557 м.
…
Высота Эрехтейон а, а также ордера
восточного портика в сумме с меньшей долей золотого сечения от его высоты
приравнена ширине портика (или всего храма): по обмеру – 8,02 м. Но это 26 оф
= 8,026 м.
…
Антаблемент приравнен половине малого
отрезка золотого сечения всей высоты ордера: по обмеру то же – 1,53 м. Но это
5 оф = 1,544 м.
…
Диаметр колонны под капителью равен
архитраву – 0,63 м (по обмеру также 0,63 м). Но это 2 оф = 0,617 м.
…
Более того, быть может, следует г. ф.
измерять Парфеноном, а не наоборот. Во всяком случае, несомненно, что именно
100 г. ф. явились исходным для последующих построений в соответствии с
трактатом Витрувия…
Пантеон. Грандиозный купольный храм с
обширным портиком хорошо сохранился до наших дней. Он расположен на небольшой
площади современного Рима, затесненной улочками и переулками. Жилые дома,
измельченные множеством окон и промежуточных карнизиков, контрастируют с
крупными архитектурными формами Пантеона. Кажется, что храм сооружен для
высших целей и не имеет отношения к повседневным заботам человека. Окон у
храма нет, освещается он круглым отверстием, обращенным в небо,
расположившимся в центре купола. Однако интерьер храма не следует сравнивать
с каким-то гротом или пещерой. Совсем нет, отверстие вверху как бы сближает его
с небосводом, придает ему "космический характер". Большой глубокий
16-колонный портик отчуждает храм от окружающего его пространства и в то же
время служит промежуточным звеном между интерьером храма и внешним миром.
Идея
произведения – замысел зодчего, архитектурно-образный строй храма заключается
в его куполе, имеющем диаметр, равный 43,2 м (140 оф = 43,219 м) <…>
Ширина портика Пантеона, измеренная изнутри, т.е. без учета толщины колонн,
равна тем же 100 г. ф. Портик выступает за пределы ротонды так, что в его
пределах вписывается квадрат, равный квадрату, определившему размер ротонды и
смежный с ним, и также имеющий сторону, равную 100 г. ф. Любопытно, что
диаметр ротонды плюс глубина портика оказываются равными по длине Парфенону.
<…> Высота Пантеона до верхнего карниза приравнена 100 г. ф. Портик по
ширине соотносится с диаметром как 3 : 5. <…> Наличие установившихся
традиций в сооружении купольных зданий может быть наглядно подтверждено,
например, сравнением Пантеона с купольным залом в термах около Бай,
сооруженным еще во 2-ой половине I в. до н. э., т.е. за два столетия до
Пантеона. Тот зал освещался так же как Пантеон, через отверстие в зените
купола. Его диаметр был ровно в два раза меньше купола Пантеона и равен 21,55
м, следовательно, сторона вписанного квадрата была равна 50 г. ф.
…
Базилика
Максенция. Ширина
базилики изнутри равна 200 г. ф., при ширине каждого поперечного нефа 100 г.
ф. Именно этот размер является исходным размером построения архитектурной
формы базилики.
Соотношение
ширины базилики и ее длины в интерьере равно отношению стороны квадрата и его
диагонали. Эти соотношения в сопоставлении друг с другом определяют толщину
опорных пилонов.
…
Храм
Софии в Константинополе. настоящее время купол имеет
диаметр, равный в направлении восток - запад 31,24 м и в направлении север -
юг – 33,04 м. Обмеры разрезов храма Св. Софии фиксируют значительные
отклонения стен от вертикали.
Первоначальный
купол, упавший во время землетрясения, был выполнен как продолжение
сферической поверхности парусов и таким образом был менее чем полусферой и
более плоским, чем купол, сооруженный позднее. Мы же должны, устанавливая
диаметр первоначального купола, приравнять его стороне подкупольного
квадрата, измеренного по основанию стен. Стороны подкупольного квадрата по
вышеупомянутому обмеру равны удивительно точно 30,8 м.
<…>
Любопытно
проследить, что если диаметр купола храма Св. Софии равен 100 г. ф. (30,8 м),
то купол храма Сергия и Вакха, а также храма св. Ирины, приравнены 50 г. ф. Среди
византийских храмов можно встретить примеры такого размера диаметра главного
купола, который выражен в округлом числе того же г. ф. Например, диаметр
купола ц. Св. Андрея в Суде VI в. (Коджа Мустафа-паша Джами) равен 20 г. ф.
(6,16 м), диаметр купола ц. Петра и Марка IX в. (Аттик Джами) – 15 г. ф. (4,6
м), диаметр купола церкви Марии Панохранты монастыря Липса X в. (Фенари-Исса)
– 12 г. ф. (3,7 м), ц. Спасителя Пантепойта XI в. (Эски Имарет Меджиди) – 15
г. ф. (4,6 м), ц. Св. Иоанна в Труле XII в. (Ахмет паша Меджиди) – 12 г. ф.
(3,7 м) и т. п.
Храм Св. Софии в Киеве. В строгом соответствии с рекомендациями Витрувия, мы начинаем
с первичного размера, заданного заказчиком или установленного зодчим. Этим
размером был диаметр купола или сторона подкупольного квадрата Софии Киевской
— 7,70 м, или 25 г. ф. <…> Необходимо отметить, что ширина, а равно и
длина храма, измеренная без галерей, но с наружными пилястрами, равна 100 г.
ф. Ширина галерей, окружающих храм, определяется тем же приемом, что и ширина
малых нефов. В итоге, изнутри длина храма с галереей относится к его ширине
так же с галереями, как высота в равностороннем треугольнике относится к его
стороне.
(Примечание от А. Ч.: А. В. Радзюкевич
на форуме «Лаборатория “золотого сечения”» пишет: «По Спасу в
Переяславле-Залесском вполне могу согласиться с Черновым. Вполне возможно,
что центральный неф был приравен 16 футам, а боковые – 12. Вполне возможно.
Любопытно, что в Софии киевской размер боковых нефов также равны 3,7 м
(обмеры мои собственные). А центральный неф равен 7,7м, что можно приравнять
25 таким футам».) http://www.a3d.ru/disput/61
Храм Св. Софии в Новгороде. Перекрытие второго яруса
многоцентровой полуаркой большого пролета (6,16 м; 20 оф – 6,174 м).
<…> Подкупольный квадрат, имеющий сторону, равной диаметру купола,
является "началом" последующих построений и приравнен 20 г. ф., или
6,16 м. Восточная сторона подкупольного квадрата равна 6,28 м, южная – 6,23,
западная – 6,24 и северная – 6,19 м. Неувязка невелика, но все же отражается
на последующих построениях.
Диаметры
купола и барабана главы равны 6,10 - 6,16 м. <…> Высота храма с
некоторым приближением, обусловленным неувязками в построении, равна его
длине. Высота храма равна 100 г. ф.
ВЫВОДЫ
К. Н. АФАНАСЬЕВА:
Мы,
анализируя пропорции сооружений исторического прошлого, как бы наблюдаем за
действиями зодчего. Он не прибегает к измерению частей здания, а он строит их
на основе простых законов соразмерности; он в принципе прибегает к мерам
длины лишь однажды, определяя исходный размер для последующей цепочки
соразмерностей. Во всем этом мы имели возможность убедиться. Этот размер
определялся "по образцу", примеру ранее сооруженных зданий и
выражался округлым значением мер длины. Мы встретились со 100-футовым
размером Парфенона; через шесть веков (!) тот же 100-футовый размер применен
строителями Пантеона Рима; еще через два века в том же Риме сооружается
базилика Максенция и ее размер определяется теми же ста футами; еще через два
века купол Софии Константинопольской оказывается равным тем же 100 г. ф.;
София в Салониках имеет размер, равный 100 г. ф.; София Киевская и София
Новгородская, так же как София в Салониках, имеют 100-футовые размеры. Те же
100 футов встречаются еще и еще во многих случаях. Б. М. Полевой в труде
"Искусство Греции "(М., “Искусство”, в 3-х томах, 1970-75.) вслед
за нами приводит много примеров использования в греческой архитектуре все
того же "сакраментального", как он называет, размера в 100
греческих футов.
Мы накопили много примеров
использования этого размера. Факт распространения этой меры – ста греческих
футов – во времени от Парфенона V в. до н. э. до Киевской Руси XI-XII веков
н. э. и на территории от Рима до Новгорода свидетельствует о своеобразной
градостроительной дисциплине, единой шкале масштабности и устойчивости меры
длины.

ПАРФЕНОН. ФРАГМЕНТЫ ЧЕРТЕЖЕЙ НИКОЛАОСА
БАЛАНОСА
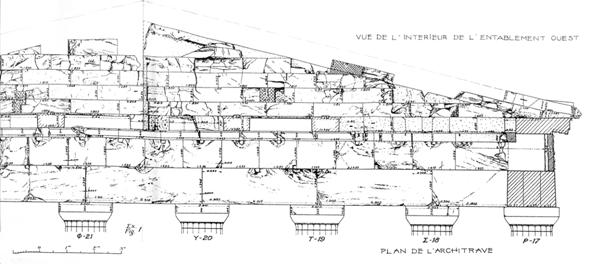
ФРАГМЕНТ ЗАПАДНОГО ФРОНТОНА
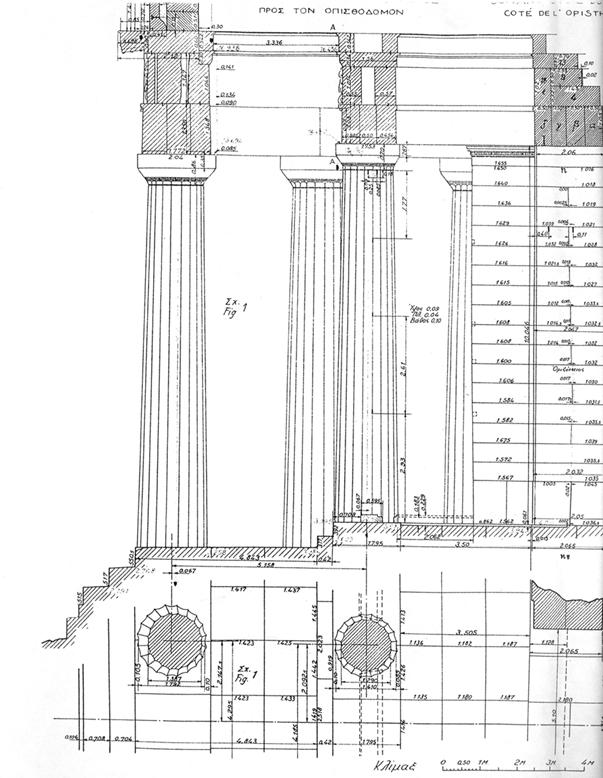
КОЛОННЫ
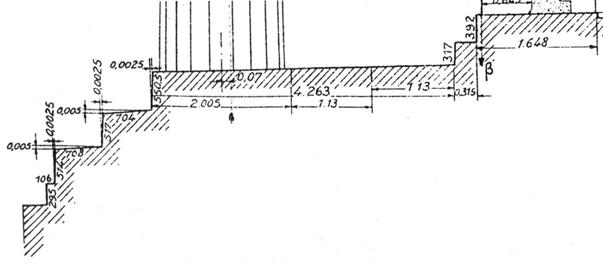
ОСНОВАНИЕ УГЛОВОЙ КОЛОННЫ
О ЧЕМ
УМОЛЧАЛ ВИТРУВИЙ
Костромской исследовать золотой
пропорции Иосиф Шефтелевич Шевелев на основе √5 составил
пропорциональное древо Парфенона[1]. Он
утверждает, что, последовательно умножая на 1 : √5, из размера высоты
ствола колонны можно получить высоту капители. Ряд выстраивается такой: высота ствола колонны – шаг колонны –
диаметр колонны – высота капители.
И
действительно, отрезок 9,57 м трижды умноженный на 1 : √5 даст отрезок
в 0,856 м, что лишь на 4 мм меньше, чем реальная высота капители.
Однако
средние члены (шаг колонны и ее диаметр) также отличаются от ожидаемых.
По формуле
Шевелева надо: 9,57 – 4,28 – 1,914 – 0,856 м
А по
обмерным планам перед нами ряд: 9,57 – 4,291 – 1,907 – 0,86 м.
Критикуя построения
Шевелева, новосибирский архитектор Андрей Радзюкевич пишет:
«Попробуем ответить на такой вопрос – если исходный размер –
ширина стилобата, равна 100 футам, то, как из него можно получить размер
высоты антаблемента? Судя по схеме дерева пропорций Шевелева, этот размер по
прямой ветви получить можно, но неизвестно какие при этом следует
использовать пропорциональные коэффициенты. Похоже, что автор тоже этого не
знает, так как приводит эту схему в
разных изданиях и нигде не дает никаких пояснений. Можно, конечно,
предположить, что высота антаблемента получается как разница между размерами
высоты ордера и полной высоты колонны, значения которых у И.Ш.Шевелева
определены. В этом случае потребуется целый ряд ”легких движений руки” с
циркулем:
1. Определяется высота ствола колонны
умножением ширины стилобата на
1 / (√5 + 1)
2. Определяется нижний диаметр колонн
через уменьшение высоты ствола колонны
в пять раз;
3.Определяется высота капители через
умножение нижнего диаметра колонн на величину
1 / √5
4. Определяется полная высота колонны
путем сложения высоты тела колонны и высоты капители.
5. Определяется высота ордера через
коэффициент (1 / √5);
6. Определяется высота антаблемента
через вычитание высоты колонны от высоты ордера
Произведя в итоге всю эту массу вычислений, получаем, что
высота антаблемента должна быть равна 0,1105573 от исходных ста футов.
Проверим это соотношение на точность. Умножив ширину стилобата на полученный
коэффициент, получаем размер 3,415 м, который больше расчетного на 11,81 см,
т.е. почти на целых 12 сантиметров. <…>
Мало
того, что полученный способ неточен. Он чудовищно громоздок…»[2].
На самом деле, все
совсем не так страшно и громоздко, как это представлено. Речь-то всего-навсего о трех элементарных
делениях и одном сложении. Однако настораживает то, что получаемые размеры
«гуляют» в обе стороны – они то больше, то меньше ожидаемого, а, значит, на
счет неточности целочисленного приближения ошибки не списать.
Уже
первое вычисление даст нам отклонение от реального размера в 3 мм.
Второй
шаг, впрочем, выправит положение, и диаметр колонны получится ровно таким,
каким и должен быть – 1,908 м.
Результат
третьего вычисления безукоризнен.
Однако
с четвертым шагом происходит и впрямь что-то непонятное. Вместо того чтобы
сложить две полученные величины и получить целое (колонна с капителью), мы
зачем-то начинаем вычисление заново. Дело в том, что колонна с капителью все
же получается на 3 см ниже, чем в натуре (а это в данном случае очень
много!).
Пятый
шаг – высота ордера. Она по формуле Шевелева на 8 см выше, чем при обмерах.
И,
наконец, – высота антаблемента 3,4129 вместо 3,297 м. Здесь Радзюкевич прав:
это уже почти на 12 см больше реального.
Перед
нами, конечно, не подгонка под ответ,
но и не система, а всего лишь некая тенденция, основанная и на том, что
пропорция 9/4 дает 2,25, и на том, что само золотое сечение есть функция от √5.
КАК ПРОЕКТИРОВАЛИ ПАРФЕНОН
Модуль Парфенона
отличается от модуля Витрувия, как алгебра от арифметики. Потому что у
замкà, запирающего эту тайну, иррациональная природа. А вот ключи к
нему могут быть и натуральными, то есть целочисленными.
Напомню, что
иррациональные, и потому и непостижимые для сознания древних √2 и √5
привели к первому кризису античной философии. Поскольку понять иррациональное
невозможно по определению, греки обожествили и квадратные корни, и золотое
сечение. Наглядное доказательство этого обнаружила искусствовед Н. М.
Введенская: стоит вписать в чертеж фасада Парфенона два прямоугольника со
сторонами √5 к 1 и √2 к 1, чтобы тут же определить и шаг колонн,
и нижний диаметр рядовой колонны, и высоту колонны с капителью.
Нижний
диаметр рядовой колонны:
100 оф : 10Ф = 1,908 м
(По плану
Баланоса 1,907 м, что можно объяснить эффектом выветривания.)
Шаг рядовой
колонны это 100 оф : 10Ф ∙
2,25 = 4,293 м
По плану
Баланоса средний шаг рядовых колонн 4,295 м, и это говорит об использовании
целочисленных отношений при переводе чертежа в камень. Реальный размер пяти
шагов рядовых колонн отличается от теоретически рассчитанного лишь на 12 мм
(21,476 вместо 21,464 м). При таком алгоритме, скорее всего, вместо Ф использовалось отношение 55/34.
(Обозначим его Ф*)
Три шага
рядовой колонны + нижний диаметр колонны приравняем к √2.
Пять шагов
рядовой колонны + нижний диаметр колонны приравняем к √5.
Это будут
горизонтальные стороны наших прямоугольников.
Ну а единица
– высота колонны с капителью (10,43 м).
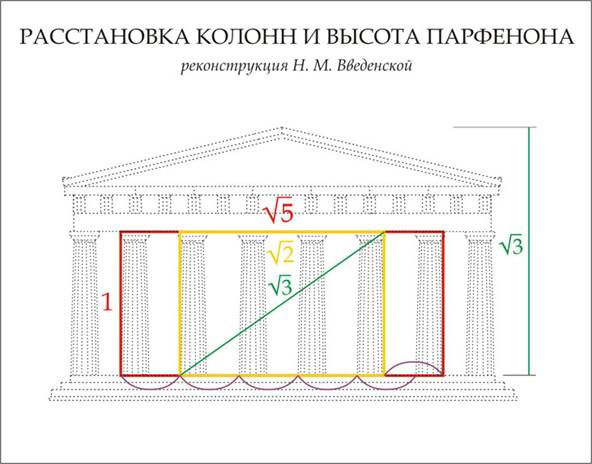
РАССТАНОВКА КОЛОНН И ВЫСОТА ПАРФЕНОНА
Итак, прямоугольник со сторонами √2 к 1 (желтый) вписан в
прямоугольник √5 к 1 (красный).
Разница между горизонтальными размерами прямоугольников определит шаг
рядовой колонны.
А диаметр рядовой колонны равен остатку после пяти таких шагов.
Диагональ прямоугольника с длинной стороной, равной √2, даст √3.
Это и будет высотой Парфенона, взятой от поверхности стилобата.
В натуре при расстановке колонн достигнута удивительная
точность: по обмерам пять шагов плюс нижний диаметр колонны дают 23,383 м, а
три шага четырех центральных колонн с одним нижним диаметром 14,793 м.
Отношение этих величин отличается от отношения √5/√2 лишь на три
десятитысячных.
Такого же порядка и определенная, видимо,
по целочисленному приближению к √2, (равному 17/12) величина колонны с
капителью
Так в середине V в. до н. э., спустя всего
полстолетия после смерти Пифагора, проблема иррациональности оказалась не
только разрешена, но и воплощена в величайшем из архитектурных шедевров
античного мира. Скульптор Фидий вместе с зодчими Иктином и Калликратом самими
пропорциями Парфенона словно бы говорили современникам: да, мы не можем
понять божественной природы иррационального, но мы научились строить,
используя его закономерности. (И за это мы также должны быть благодарны
Гиппасу из Метапонта.)
При таком
геометрическом построении неясно, как именно высота колонны с капителью
связана с шириной стилобата и высотой ордера.
Однако
высота ордера, деленная на 29/26 (приближение к √5/2) с точностью до
миллиметра дает размер от нулевой отметки до верха капители.
МОДУЛЬ ПАРФЕНОНА
Стилобат
– 100 олимпийских футов по 0,30871
м или 63 дорийских локтя по 0,49 м
Высота
ордера 100 оф : 2,25 или 28 дорийских локтя
Нижний диаметр рядовой колонны фасада (со второй по
седьмую):
100 оф
: 10Ф = 1,908 м
Ф –
золотое число 1,618…
Шаг рядовых колонн:
Диаметр
колонны, умноженный на
2,25 = 4,293 м (в натуре средний шаг
4,295 м )
При
высоте колонны с капителью, принимаемой за единицу, три шага колонны +
диаметр колонны = √2, а пять шагов колонны + диаметр колонны = √5.
СВЯЩЕННЫЙ ЕГИПЕТСКИЙ ТРЕУГОЛЬНИК 3-4-5
Священный треугольник может
быть вписан в чертеж фасада Парфенона несколькими способами. Наиболее
интересным, пожалуй, является такой: длинный катет задан высотой ордера (28 дл), а короткий равен
1/3 ширины стилобата (21 дл).
Если
поставить этот треугольник на стилобат так, чтобы одна из его вершин
коснулась основания угловой колонны (ее нижний диаметр 4 дл), то длинный
катет начнется от основания четвертой колонны.

Наличие
священных треугольников может и не говорить о способе проектирования. В ряде
случаев перед нами, скорее всего, будет лишь дань популярному отношению 3/4.
Однако в данном случае графические совпадения слишком красноречивы, чтобы
быть просто совпадениями, ведь они определяют ширину первого межколонья и
сумму высоты ордера с высотой основания.
ПЛАН ПАРФЕНОНА
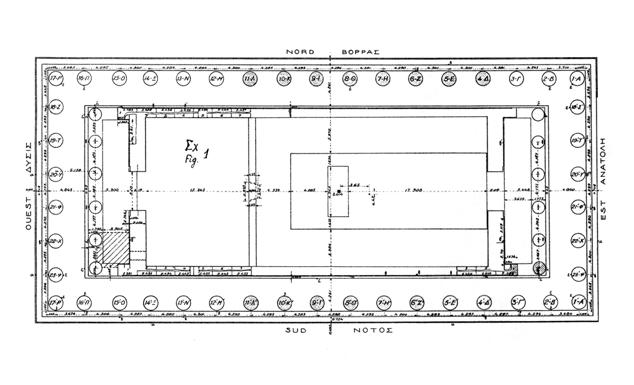
ПЛАН ПАРФЕНОНА ПО БАЛАНОСУ
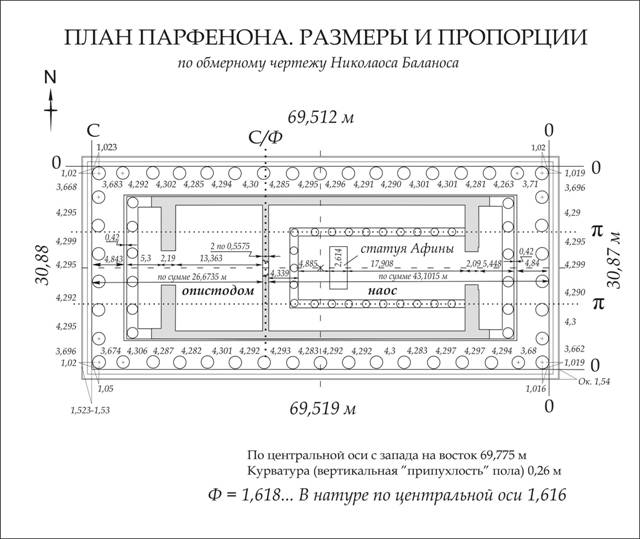
Святилище
поделено на два помещения пропорцией С/Ф
(с точностью 1,616).
Ряды колонн
внутри святилища расчислены, вероятно, по числу π. Этот же
пропорциональный принцип будет заложен и в римской Арке Константина, в церкви
Успения в Старой Ладоге середины XII в. и Петропавловском соборе
Доменико Трезини.
Все это – лишь
геометрия. Как реализовать ее в натуре? Как перевести иррациональные
величины, так легко получаемые на чертеже при помощи диагоналей квадратов и
полуквадратов, в футы и локти?
Напомним,
что древние не умели высчитывать значения квадратных корней, и пользовались
или геометрическими построениями, или целочисленными приближениями.
Парфенон
это и демонстрирует:
Если ширину
стилобата (30,87 м) умножить на √5, то мы получим длину стилобата с
отклонением в 48,5 см. Однако заменим √5 целочисленным приближением
9/4, и длина здания будет лишь на 5,6 см более идеального (при размере в 70
метров, да еще с учетом того, что за две с половиной тысячи лет постройка
выдержала не одно землетрясение, это вполне приемлемо).
Еще пример:
высота карниза 0,6 м; высота архитрава 1,350 м.
0,6 м ∙
√5 = 1,342 м; Откл. 8 мм
0,6 м ∙
2,25 = 1,35 м; Откл. 0
Значит, мы
должны иметь дело с целочисленным приближением к квадратным корням (Таблицу
целочисленных приближений к иррациональным константам и более подробный
анализ пропорций Парфенона см. в конце этой главы).
Произведем
расчет по целочисленному приближению к √2 (17/12) и Ф*, целочисленному (55/34) приближению
к числу Ф.
1).
Умножаем 100 оф (или 63 дл) на 2,25 и получаем длину стилобата.
2). Делим
100 оф (или 63 дл) на 2,25 и получаем высоту ордера (от верха стилобата до
фронтона) 13,728 м[3]
3). Делим
100 оф на 10Ф и получаем нижний
диаметр рядовой колонны.
4). Нижний
диаметр рядовой колонны, умноженный на 2,25, дает шаг рядовой колонны по
ширине стилобата.
По
геометрическому построению пять шагов колонны + диаметр колонны должен
относиться к высоте колонны с капителью как √5 к 1, а три шага колонны
+ диаметр колонны к высоте колонны с капителью как √2 к 1.
Как
выполнить это условие?
5). Взяли
расстояние, занимаемое по горизонтали четырьмя рядовыми колоннами (три шага и
толщина одной колонны) и приняли за длинную сторону прямоугольника со
сторонами √2 : 1. Поделили на 17/12 (приближение к √2) и получили
высоту колонны с капителью – 10,43 м.
Обмер и дает эту величину. (Удвоенная величина колонны с капителью
будет относиться к трем шагам колонны по Ф.)
6). Высота
ордера, деленная на √2, даст высоту каннелюров (высота ствола колонны с
шейкой).
7). Высота
каннелюров, деленная на 2,25, даст 4,3236 м. Это 14 оф (4,322 м). Таково и
расстояние от верха карниза до верха тела колонны.
Такой, если
верить геометрии, должна быть и высота фронтона (также от верха карниза).
8). За
нижний диаметр угловой колонны берем сторону модульного квадрата в 4
дорийских локтя. Нижний диаметр угловой колонны, умноженная на 2,25, дает шаг
рядовой колонны, но уже по длине стилобата[4].
Однако это
лишь начальный этап проектирования. После этого за счет членения антаблемента
и прибавления стереобата следует то, что можно назвать «золотой настройкой».
Попытки найти в пропорциях
Парфенона золотое сечение регулярно предпринимаются с середины XIX столетия
(первым в середине XIX
в. был немецкий биолог А. Цейзинг).
А. В.
Радзюкевич сообщает:
«По его предположению высота колонн Парфенона в сумме с
высотой стилобата относится в ”золотом сечении” к высоте антаблемента в сумме
с высотой фронтона.
(10,43
+ 1,59) : (3,29 + 4,26) = 12,02 : 7,55
= 1,592
Получается коэффициент довольно близкий к ”золоту”».
Но высота стилобата
от нулевой отметки не 1,59, а 1,887 м (вместе с высотой колонны, взятой с
капителью, это 12,317 м), а высота фронтона с антаблементом по нашим расчетам
7,619 м. Исследователь почему-то просто проигнорировал евтентерий – нижнюю
ступеньку Храма. Итак:
12,317 :
7,619 = 1,617 → Ф
Радзюкевич,
резкий и последовательный противник гипотезы об осмысленном использовании
золотого сечения в архитектуре античности и средневековья, в своей
диссертации пишет о методологии исследования архитектурных форм, разработанной
во второй половине XX
в. Джим Коултоном: «Наиболее наглядно
метод Дж. Коултона можно продемонстрировать на выявленном им правиле
классического периода. По этому правилу размеры стилобата определяются через
рядовой шаг колонн».
Но так и
утверждал Витрувий, полагавший, что у одного из видов «правильных храмов»
диаметр колонны, умноженный на два с четвертью, дает шаг колонн[5].
Применим
методику Витрувия к Парфенону. Оказывается, проще всего взять за базовый
размер то, что базой и является – ширину стилобата:
Если ее
умножить на два с четвертью, то получим длину стилобата. Если ширину
стилобата поделить на два с четвертью, то получим высоту ордера.
Если
поделим ту же ширину стилобата на 10 ´ Ф, то определим диаметр рядовой
колонны 1,908 м. А, умножив диаметр рядовой колонны на два с четвертью,
определим шаг рядовых колонн (4,295 м).
Если взять
диаметр угловой колонны, равной 4 дл и умножить его на два с четвертью, то
получим шаг колонн по длине стилобата.
Выходит,
пропорции Парфенона ориентированы на пропорцию 9/4 (то есть два с четвертью)
и те, которые мы сегодня называем золотыми. Только пользовались древние
мастера, видимо, не иррациональным числом 1,618…, а числом Ф* (т. е. отношением 55/34).
ШКАЛА ЗОЛОТОЙ ЛИНЕЙКИ
Пытаясь целочисленно выразить
геометрическое золото, античные геометры должны были действовать простым
перебором. Геометрически построив отрезок, древний математик должен был найти
величину, кратную его частям.
Предположим,
отрезок в три олимпийских фута (0,92613 м) – это диагональ некоего полуквадрата.
Геометрически по золотому сечению он делился на два: 0,57238 и 0,35375 м. Вот только, работая
циркулем, чисел мы не получим. И линейка с мерной шкалой нас тоже не выручит,
поскольку мерной шкалы еще нет, и ее только надлежит разбить.
Первое приближение
к золотому сечению дает деление отрезка на 13 модулей (пропорция 8 : 5).
Однако 0,567 м (таковы восемь модулей
при делении трех футов на 13 частей) отличны от геометрической длины большего
отрезка почти на 2,4 мм.
Ошибка
бросается в глаза.
При делении
трехфутового отрезка на 21 модуль, отношение 13 к 8 даст погрешность в 0,9
мм, а при 34 модулях получим едва различимое глазом отклонение в 0,4 мм.
И только
поделив общий отрезок на 55 частей (по 0,0168 м), математик должен был
обнаружить, что в большей части 34 деления (0,57252 м), а в меньшей их 21
(0,35361 м)
Обнаружить
отклонение в 0,14 мм даже при тщательном построении нереально.
Уточним размеры Парфенона по
золотому сечению.
По А. В. Радзюкевичу
высота Парфенона должна быть 40 дл. Жаль только, что с учетом высоты
евтентерия (тонкой надземной части лежащей под храмом нижней плиты) это
красивое число превращается в 40,6 дл (19,907 м). При этом высота ордера
(антаблемент + колонны с капителью) по обмерам – 13,728 м (28 дл).
Но удвоим
высоту колонны с капителью (2 ∙ 10,43 м = 20,86 м) и, начиная с этого размера, станем
последовательно делить на число Ф* (то
есть 55/34):
20,86
: Ф* =
12,895 м (три шага колонны = 12,885 м)
: Ф* =
7,972 м (фронтон
+ антаблемент + абак = 7,97 м)
: Ф* =
4,928 м
(фронтон + карниз = 4,923 м)
: Ф* =
3,046 м (фриз
+ архитрав + абак = 3,048 м)
: Ф* =
1,883 м
(стереобат с евтентерием = 1,887 м)
: Ф* =
1,164 м
(толщина боковых стен наоса, то есть помещения самого храма = 1,16)
А поделив
высоту антаблемента (3,297 м = карниз + фриз + архитрав) на Ф*, получим 2,038 м. Это толщина
торцевых стен наоса.
Это говорит
о том, что вертикальные размеры Парфенона и впрямь расчислены по золотому
сечению. Но в случае с фронтоном и карнизом, а также с членением более мелких
деталей (к примеру, капителей) строители пользовались не целочисленным
переводом иррациональных величин в целочисленные, а шнуром, позволявшим
избежать ошибки перевода.
Высота стереобата с евтентерием
должна была настроить вертикальные пропорции фасада на золото.
Итак,
основные пропорции вертикали фасада и впрямь оказываются золотыми.

ЗОЛОТОЕ СЕЧЕНИЕ ПАРФЕНОНА
При этом нужно добавить, что пропорция W/D, то есть три шага колонны к высоте колонны с капителью, дают
пропорцию 2/Ф, и если брать по
обмерам Баланоса, то отклонение ничтожно (1,2354 вместо 1,2361), а пять шагов
колонны к высоте тела колонны дадут 2,24, то есть приближение к √5.

ВЫСОТА КАПИТЕЛИ РЯДОВЫХ КОЛОНН ПАРФЕНОНА
У современных
Парфенону дорийских храмов в Пестуме пропорциональная проблема видна
невооруженным взглядом: толстые колонны, напоминающие ноги персидских боевых
слонов и тяжелый верх. В Парфеноне эта проблема решена с помощью целочисленного
приближения к √2, √5 и золотой пропорции. Но, как это ни странно,
в пестумских храмах используются те же пропорциональные принципы. И на
чертеже все выглядит весьма привлекательно. Однако только на чертеже.

ХРАМ ГЕРЫ В ПЕСТУМЕ. ПРОПОРЦИОНАЛЬНАЯ ПРИКИДКА
Cамо по себе
использование иррациональных и трансцендентных констант к гармонии не
приводит. То, что может быть красиво на плоскости, при механическом
использовании приема (ради самого приема) в объеме зачастую превращается в
нечто мертвое и тяжеловесное.
Почему в одних пропорциях гармонические константы вступают в диалог и
составляют некое новое парадоксальное единство, а в других рассыпаются, мы
пока не знаем. Впрочем, ни золотое сечение, ни другие гармонические константы
на фасаде этого храма зрительно не акцентированы.
В любом искусстве стиль – это способ сворачивания пространства.
Архитектуру недаром называют застывшей музыкой, ведь в ее объектах свернутым
(а потому и почти что отмененным) оказывается время. Потому-то в Гизе и было
когда-то сказано, что время боится вечности, а вечность боится пирамид.
МАТРИЦА ЗОЛОТОГО
СЕЧЕНИЯ
На потолочных
плитах Парфенона был выгравирован орнамент с пропорциональной матрицей. В ней
и следует искать разгадку мерных отношений храма.

ПАРФЕНОН.
МАТРИЦА ЗОЛОТОГО СЕЧЕНИЯ
В центре матрицы
довольно экзотические для Греции растения – цветок лотоса и метелка папируса.
Цветок лотоса символизирует здесь сторону квадрата, а побег папируса
– его диагональ (то есть прямую и “косую” меру).
Высота стебля лотоса (от центра квадрата до бутона) равна высоте
бутона.
Вспомним, что Пифагор учился математике в Египте.
Хотя рисунок оправлен меандром, то есть типично греческим орнаментом,
растительные реалии свидетельствуют, что идею золотого сечения греки
заимствовали у египтян. Тем более, что в Египте со времен V династии капители
колонн делались или в виде лотоса, или в виде метелки папируса.
Цветок лотоса был геральдическим знаком Верхнего Египта, а стебель
папируса Египта Нижнего. Поэтому, надо думать, перед нами растиражированный в
мраморе чертеж египетских жрецов.

Рамой рисунку – меандровый орнамент. Всмотримся в его линии. Прямоугольник
двойного квадрата (4 на 8 олимпийских футов) проходит по центру окаймляющего
рисунок меандра.
Вот как будет выглядеть матрица Парфенона, если оставить на чертеже
лишь голую математику.
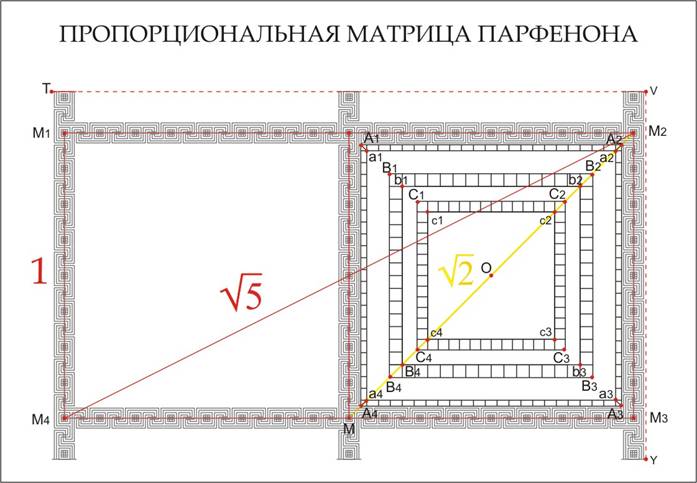
M1M2M3M4 – двойной квадрат 4 на 8 олимпийских
футов (8 на 16 шагов меандра).
A1A2A3A4 – мерная линейка со шкалой в
2 дюйма (угловые квадратики по 1 дюйму).
Длина стороны мерной линейки без двух
угловых квадратиков 7 шагов меандра или 3,5 оф.
8 светлых линий меандра – 3 дюйма, а
32 линии – 1 оф.
Диагональ двойного квадрата (M2M4)
минус короткая его сторона (M2M3) равна двойному минорному золоту, то есть √5
– 1. Но такова величина диагонали квадрата мерной линейки, взятой без двух
угловых квадратиков (a2a4).
Сторона более крупного квадрата становится
диагональю меньшего:
a3a4 = b2b4 = 3,5 оф = 42 дюйма = 7 шагов меандра
b1b2 = c2c4 = 2,5 оф = 30 дюйма = 5
шагов меандра
c1c2 = Ob4
Отношение горизонтали к вертикали по
числу линий таково, что если размер брать по габаритным точкам T,V,Y, то
267 : 165 = 3 · (89 : 55) = 1,6182...
Следовательно, TV : VY – целочисленное
приближение к золотому сечению через два смежных числа ряда Фибоначчи.
Однако для того, чтобы ответить, как пользовались древние зодчие
пропорциональной матрицей, нужны специальные разыскания и исследования.
Шаг меандра (от одной крестчатой розетки до другой) в натуре равен
½ олимпийского фута.
С внутренней стороны меандрового квадрата находится измерительная
линейка со шкалой в два дюйма (угловые квадратики шкалы – по дюйму).
Высота вертикальных мачт равна диагонали квадрата измерительной
линейки.
Короткая сторона меандрового прямоугольника равна диагонали среднего
квадрата (взятой по внешней стороне рамы из стилизованных лепестков).
Сторона малого квадрата (с рисунком внутри его) – диагональ среднего
квадрата.
(Внешняя сторона малой лепесковой рамы, в два раза меньше короткой
стороны меандрового прямоугольника.)
Внутренняя сторона большой лепестковой рамы – 0,62 от короткой стороны
меандрового прямоугольника двойного квадрата, а внутренняя сторона малой
лепестковой рамы – 0,62 от внутренней стороны большой лепестковой рамы.
Отношение горизонтали меандра к его вертикали равно 1,6 к 1, а
отношение ширины чертежа к высоте (с учетом «шрифтовых засечек» на концах
вертикальных мачт) дает золотую пропорцию.
Итак, мы
убедились, что расчисленный парной мерой Парфенон, – это гимн
иррациональному: квадратным корням и золотому сечению. Но имеет ли к этому
какое-либо отношение скульптор Фидий?
Очевидно, имеет.
Внутри храма стояла двенадцатиметровая статуя Афины из золота и
слоновой кости. Другая, бронзовая
статуя Афины-Промахос (Воительницы) была чем-то вроде маяка находилась
перед храмом. Моряки издалека видели, как горит копье и гребень шлема
богини-девы.
Увы, оба этих изваяния утрачены.
А. В. Радзюкевич не нашел в наследии античности примеров членения
человеческого тела по золотому сечению. Но обратимся к римской копии 1 в. до
н. э., сделанной с оригинала другого греческого скульптора и современника
Фидия – Мирона. В случае с Афиной Мирона золото и впрямь приходится на пряжку
пояса богини, то есть на пупок. Может быть, потому, что на голове у
Девы-воительницы высокий шлем.

Древнегреческую поговорку «В
Афины со своей совой» (сова была символом Афины, а потому и носящего ее имя
города) мы знаем по русской кальке «В Тулу со своим самоваром». Но есть и
другая русская реплика на античный оригинал: «В чужой монастырь со своим
уставом».
Последнего
сами греки не боялись. Они знали законы пропорции. Археологи обнаружили
несколько античных пропорциональных циркулей. Один из них, помпейский,
настроенный на золотое сечение, сегодня хранится в Неаполе. Его длина 14,6 см
делится шарниром на отрезки 5,6 и 9 см. Три других циркуля найдены в Риме. Циркуль
длиной 21,9 см разделен на отрезки 14,6 и 7,3 мм[1],
а циркуль длиной 20,1 см на отрезки 13,4 и 6,7 см (оба настроены на пропорцию
2 к 1). Циркуль Музея Терм в Риме (14,6 см) разделен на отрезки 9,4 и 5,2 см,
то есть, как показал И. Ш. Шевелев, установлен на отношение √5 : (√5
– 1).

Римская
арка императора Константина свидетельствует, что архитекторы античности
проектировали свои шедевры не на основе примитивной арифметики Витрувия, а по
корням из двойки и пятерки, золотому сечению и числу π.
2008 – 2009
Приложение 1.
ПАРАМЕТРЫ И
ПРОПОРЦИИ ПАРФЕНОНА
ОБЩИЕ РАЗМЕРЫ
1. Ширина стилобата (плита, на
которую опираются колонны) – 30,87 м = 100
оф = 63 дл
Дорийский локоть в 0,4903 м вычислен не по √2, а по
целочисленному приближению к нему (17/12).
В идеальном случае при 1оф = 0,30871 м он должен равняться 0,4912 м.
2. Средняя длина стилобата –
69,515 м
100 оф ×
2,25 = 69,46 м; (в натуре больше на 5,5 см)
Альтернативный вариант вычисления через
дорийский локоть (0,4903 м):
63 дл = 30,89 см
100 дл ×
17/12 = 69,459 м;
63 дл ×
2,25 = 69,5 м; (в натуре больше на 1,5 см)
63 дл длинней 100 оф лишь на 1,8 см. Длина
стилобата могла быть расчислена и футом, и локтем. Видимо, именно это
сближение двух мер и привлекало строителей.
2. Ширина евтентерия – 33,96 м,
то есть 110 оф.
3. Высота Парфенона (от нулевой
отметки евтентерия) – ок. 19,94 м и высота фронтона ок. 4,32 м
Верх фронтона разрушен, и обмерные чертежи
дают лишь предположительную величину, вычисляемую по углу схода кровли. Геометрически
высота фронтона с точностью до 3 см будет равна 4,32 м (но 4,322 м – 14 оф).
При этом высота фронтона с толщиной лежащего под ним карниза равна
рассчетному шагу рядовых колонн – 4,923 м. При таких величинах отношение
высоты храма к высоте верхней точки капители, взятой от нулевой отметки, дает
золотое сечение с точностью 1,619. А кроме того, высота каннелюров (колонна с
шейкой капители), деленная на 2,25, даст 14 оф, т. е. высоту фронтона
(погрешность 1,5 мм).
4. Вертикальный обмер от низа евтентерия
до верха антаблемента:
1,887 м + 10,43 м + 3,297 м = 15,614 м
Через двузначное приближение к √2
это можно выразить так:
2,25 × 10 дл ×
17/12 = 15,628 м
КОЛОННА
1. Высота ствола колонн – 9,570 м = 31 оф
Ширина стилобата 100 оф, а 100 : 31 есть целочисленное приближение к (√5 + 1).
(В дорийских локтях высота ствола колонны Парфенона целочисленно не выражается.)
2. Высота капители – 0,86 м
Высоту капители можно получить, построив
полуквадрат с короткой стороной в 2,25 оф (два фута и три дюйма при дюйме в
1/12 фута) и вычтя от длины его диагонали размер короткой стороны. Если
строить геометрически, то высота капители будет 0,859 м, но заменим
геометрическое построение алгебраическим:
1 оф ×
2,25 × 26/21 = 0,86 м
26/21 – одно из лучших приближений к √5
– 1
3. Высота колонны с капителью –
10,43 м
15 оф ×
2,25 = 10,419 м Откл. 11 мм
15 дл ×
17/12 = 10,419 м Откл. 11 мм
4. Высота эхина и абака
(верхние части капители) – по 0,351 м
Это высота капители, деленная на √5
– 1
0,86 м : 38/31 = 2 × 0,351 м
5. а) Ширина
абака угловых колонн восточного фасада (навершие капители в виде
прямоугольной доски) – 2,085 м
3 оф ×
2,25 = 2,084 м Откл. 1 мм
3 дл ×
17/12 = 2,084 м Откл. 1 мм
И. Ш. Шевелев заметил, что ширина этих
абак равна 1/5 высоты колонны с капителью.
б) Средняя
ширина абак рядовой колонны восточного фасада – 2,058 м
15 оф : 2,25 = 2,058 м Откл. 0
6. Высота шейки капители –
0,158 м; высота тела колонны с ней 9,728 м
14 дл ×
17/12 = 9,724 м; Откл. 4 мм
Высота тела колонны с шейкой капители
9,728 м. Умножим это число на 2,222… и получим ровно 70 оф (такой могла быть
высота фасада со скульптурной группой на фронтоне).
7. Нижний диаметр угловой
колонны – 1,96 м. Это сторона модульного квадрата в 4 дорийских локтя.
Угловые колонны толще рядовых. Это создает
иллюзию того, что колонны стоят по полуокружности, выгнутой своими краями
навстречу зрителю. Отношение диаметра угловой колонны к диаметру рядовой
колонны фасада равно пропорции живого ростового квадрата 1,03 к 1
8. Нижний диаметр рядовой
колонны – 1,908 м
100 оф : 10Ф* = 1,908 м
Ф* – целочисленное золотое приближение
55/34
9. Шаг рядовых колонн
(пятикратно со второй по седьмую) – 4,295 м
10 оф
: Ф* × 2,25 = 4,294 м
10. Нижний диаметр колонн малых
алтарей Парфенона – 0,442 м
1 оф, умноженный на 10/7 (целочисленное
приближение к √2) Откл. 1 мм
ОРДЕР
1. Высота антаблемента +
колонны с капителью – 13,728 м (28 дл). Высота
колонны с капителью плюс антаблемент относится к высоте ствола колонны, взятой
с шейкой капители (9,728) по √2 в целочисленном приближении 24/17.
Но
16 оф ×
2,25× 21/17 =
13,7285 м
АНТАБЛЕМЕНТ И ФРОНТОН
1. Высота антаблемента (карниз
+ фриз + архитрав) – 3,297 м
3 дл × 65/29
= 3,297; Откл. 0
где 65/29 – целочисленное приближение к √5
2.
Архитрав (1,35 м; прямоугольная балка, лежащая на колоннах) + фриз (1,347 м;
балка, лежащая между карнизом и архитравом) = 2,697 м
5,5 дл = 2,697 м
3. Высота карниза – 0,6 м.
Расчет от архитрава:
1,35 м : 2,25 = 0,6 м; Откл. 0
5. Реконструированная высота
фронтона – 4,322 м (14 оф)
6. От от нулевой отметки до
низа подкарнизной балки (верхняя часть фриза) – 30 дл. Сумма высот от гребня
кровли до низа подкарнизной балки (фронтон с кровлей + карниз + верхняя балка
фриза) 5,212 м (это половина высоты колонны с капителью).
СТЕРЕОБАТ
1. Высота стереобата (четыре
ступени под колоннами) – 1,887 м (три верхних ступени – 1,592 м и евтентерий
– 0,295 м)
Метрологически эти размеры в целочисленном
виде не интерпретируются (6 оф + 0,02476 м). Это значит, что они получены
алгебраически. Так и оказывается:
Стереобат +
колонна с капителью
––––––––––––––––––––––––––––––– =
1,619 → Ф
Антаблемент
+ фронтон
При квадрате золотого сечения, равном
2,62:
фронтон +
карниз
–––––––––––––––––
= 2,619 → Ф2
стереобат
СВЯТИЛИЩЕ (НАОС)
1. Ширина наоса (внутреннее
помещение) – 21,534 м
31 оф ×
2,25 = 21,532 м; Откл. 2 мм
31 дл ×
17/12 = 21,532 м; Откл. 2 мм
2. Длина наоса – 48,250 м
Отношение длины наоса к ширине = 2,2406 =
65/29 (с точностью 1 : 1,0002),
след., длина наоса равна ширине, умноженной на 65/29 (или 56/25):
31 оф ×
2,25 × 65/29 = 48,263 м
Приложение 2.
ЦЕЛОЧИСЛЕННЫЕ ПРИБЛИЖЕНИЯ К
ИРРАЦИОНАЛЬНЫМ КОНСТАНТАМ
Приближения
к √2 = 1,4142136…
10 : 7 =
1,429
17 : 12 =
1,4167
24 : 17 =
1,412
41 : 29 =
1,4138
99 : 70 =
1,41429
100 : 71 =
1,41
Приближения
к (√5 – 1) = 1,236068…
21 : 17 =
1,2353
27 : 22 =
1,2273…
31 : 25 =
1,24
38 : 31 =
1,226
100 : 81 =
1,235
Приближения
к (√5 + 1) : 2 = 1,618034… (по числам ряда Фибоначчи)
8 : 5 = 1,6
13 : 8 =
1,625
21 : 13 =
1,615…
34 : 21 =
1,619…
55
: 34 = 1,6176…= Ф*
89 : 55 =
1,6182…
144 : 89 =
1,61798…
233 : 144 =
1,618056…
Приближения
к √3 = 1,732…
19 : 11 =
1,727272…
26 : 15 =
1,73333…
Приближения
к √5 = 2,236068…
9 : 4 =
2,25…
29 : 13 =
2,231…
38 : 17 =
2,2353…
47 : 21 =
2,238…
49 : 22 =
2,2273…
56 : 25 =
2,24…
65 : 29 =
2,241…
69 : 31 =
2,22581…
100 : 45 =
2,222…
181 : 81 =
2,235…
Приближения
к (√5 + 1) = 3,236068…
42 : 13 = 3,231…
55 : 17 =
3,2353…
68 : 21 =
3,238…
71 : 22 =
3,2273…
81 : 25 =
3,24…
94 : 29 =
3,241…
100 : 31 =
3,226…
262 : 81 =
3,235…
[1] 21,8 см есть греческий фут (30,87 см), деленный на √2.